FUNCIONES TRIGONOMÉTRICAS EN LA CIRCUNFERENCIA TRIGONOMETRICA

La circunferencia trigonométrica es aquella cuyo radio es 1 y su centro es el origen de las coordenadas. Al considerar el radio de una unidad, las expresiones en las que aparece éste se simplifican.  La circunferencia trigonométrica nos permite asociar segmentos al seno y al coseno.

Sen q  =  AB/OB  =  AB                                                         Csc q  =  OF/OE  =  OF                      Cos q  =  OA/OB = OA

Sec q  =  OD/OA =  OD                                                         Tan q  =  CD/OC  =  CD                                                        Ctg q  =  EF/OE   =  EF                                                          

FUNCIONES DE LOS ANGULOS DE 0°, 30°, 45°, 60° Y 90°

A continuación se muestra una tabla con los valores más importantes y utilizados en el campo de la trigonometría:

SIGNOS DE LAS FUNCIONES

RESOLUCION DE TRIANGULOS OBLICUANGULOS

Un triángulo oblicuángulo es aquel que no es recto ninguno de sus ángulos, por lo que no se puede resolver directamente por el teorema de Pitágoras, el triángulo oblicuángulo se resuelve por leyes de senos y de cosenos, así como el que la suma de todos los ángulos internos de un triángulo suman 180 grados.

LEY DE LOS SENOS:

La ley de Senos es una relación de tres igualdades que siempre se cumplen entre los lados y ángulos de un triángulo cualquiera.

Para poder utilizar la ley de los senos se necesitan los siguientes datos:

1)      Dos lados y un ángulo opuesto

2)      Dos ángulos y un lado

FORMULAS

LEY DE LOS COSENOS:

La ley de cosenos se puede considerar como una extensión del teorema de Pitágoras aplicable a todos los triángulos. Ella enuncia así: el cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos dos lados multiplicado por el coseno del ángulo que forman. Si aplicamos este teorema al triángulo de la figura 1 obtenemos tres ecuaciones:

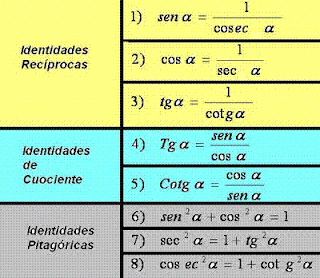
IDENTIDADES TRIGONOMÉTRICAS

Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas)

IDENTIDADES FUNDAMENTALES

Para poder demostrar una igualdad o identidad trigonométrica, debemos:

1)      Trabajar en los 2 miembros de la igualdad y llegar a un  mismo valor.

2)      Obtener una identidad fundamental.

FUNCIONES DE SUMA Y RESTA DE 2 ANGULOS

FORMULAS

sen (α +β ) = senα * cosβ + senα * cosβ

cos (α +β ) = senα * cosβ - senα * cosβ

sen (α -β ) = senα * cosβ - senα + cosβ

cos (α -β ) = senα * cosβ + senα * cosβ